Question

Expand the following using the Binomial Theorem and Pascal’s triangle. (x + 2)6 (x − 4)4 (2x + 3)5 (2x − 3y)4

In the expansion of (3a + 4b)8, which of the following are possible variable terms? Explain your reasoning. a2b3; a5b3; ab8; b8; a4b4; a8; ab7; a6b5

Answer 1

See solution

Explanation:

Use formula for the binomial expansion:

`(a+b)^n=C_n^0a^n+C_n^1a^(n-1)b+C_n^2a^(n-2)b^2+\dots+C_n^(n-1)ab^(n-1)+C_n^nb^n.`

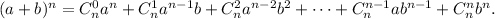
Note that
`C_n^0=C_n^n=1,\ C_n^1=C_n^(n-1)=n.`

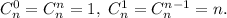
1. For the expression
`(x+2)^6:`

`(x+2)^6=x^6+C_6^1x^5\cdot 2+C_6^2x^4\cdot 2^2+C_6^3x^3\cdot 2^3+C_6^4x^2\cdot 2^4+C_6^5x\cdot 2^5+2^6=x^6+6\cdot 2x^5+15\cdot 4x^4+20\cdot 8x^3+15\cdot 16x^2+6\cdot 32x+64=x^6+12x^5+60x^4+160x^3+240x^2+192x+64.`

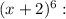
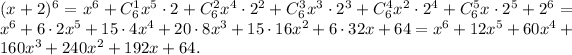
2. For the expression
`(x-4)^4:`

`(x-4)^4=x^4-C_4^1x^3\cdot 4+C_4^2x^24^2-C_4^3x\cdot 4^3+4^4=x^4-4x^3\cdot 4+6x^2\cdot 16-4x\cdot 64+256=x^4-16x^3+96x^2-256x+256.`

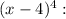
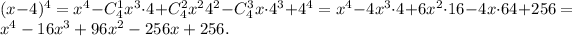
3. For the expression
`(2x+3)^5:`

`(2x+3)^5=(2x)^5+C_5^1(2x)^4\cdot 3+C_5^2(2x)^3\cdot 3^2+C_5^3(2x)^2\cdot 3^3+C_5^4(2x)\cdot 3^4+3^5=32x^5+5\cdot 16x^4\cdot 3+10\cdot 8x^3\cdot 9+10\cdot 4x^2\cdot 27+5\cdot 2x\cdot 81+243=32x^5+240x^4+720x^3+1080x^2+810x+243.`

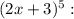
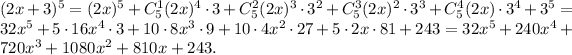
4. For the xpression
`(2x-3y)^4:`

`(2x-3y)^4=(2x)^4-C_4^1(2x)^3\cdot (3y)+C_4^2(2x)^2\cdot (3y)^2-C_4^3(2x)\cdot (3y)^3+(3y)^4=16x^4-4\cdot 8x^3\cdot 3y+6\cdot 4x^2\cdot 9y^2-4\cdot 2x\cdot 27y+81y^4=16x^4-96x^3y+216x^2y^2-216xy^3+81y^4.`

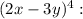
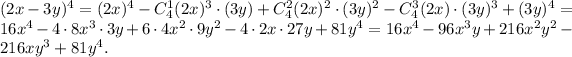
5. In the expansion of
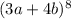`(3a + 4b)^8` each term has the degree of 8. Since product
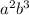`a^2b^3` has degree 2+3=5, this term is not possible. Since product
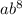`ab^8` has degree 1+8=9, this term is not possible. Similarly, term
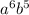`a^6b^5` has degree 6+5=11 and is not a term of expansion
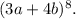`(3a + 4b)^8.` Products
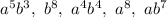`a^5b^3,\ b^8,\ a^4b^4,\ a^8,\ ab^7` have degree 8 (5+3=8=4+4=8=1+7), these products are possible terms with corresponding coefficients.