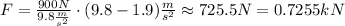Question

A person weighing 0.9 kN rides in an elevator that has a downward acceleration of 1.9 m/s^2. The acceleration of gravity is 9.8 m/s^2. What is the magnitude of the force of the elevator floor on the person? Answer in kN and round 4 decimal places.

Answer 1

The magnitude of the force is 0.7255kN

Step-by-step explanation:

The elevator floor acts on the person with a force that is due to the gravitational acceleration less the downward acceleration of the elevator:

(force of floor F) = (mass of person m) x [ (grav. acceleration g) - (elevator acceleration a) ]

in other words, considering the elevator floor as a reference frame in the Earth's gravitational field, the person's weight decreases due to the downward acceleration, as follows:

`F = m\cdot(g-a)`

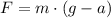
We are given the person's weight at rest, 0.9kN, from which the mass can be determined as:

`900 N = m\cdot g \implies m = (900N)/(9.8 (m)/(s^2))`

So

`F = (900N)/(9.8 (m)/(s^2))\cdot(9.8-1.9)(m)/(s^2)\approx 725.5N=0.7255kN`