Answer : The theoretical yield of potassium carbonate is, 146.483 g
The percent yield of potassium carbonate is, 85.33 %
Solution : Given,
Mass of
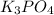 = 150 g
= 150 g
Mass of
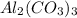 = 90 g
= 90 g
Molar mass of
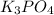 = 212.27 g/mole
= 212.27 g/mole
Molar mass of
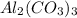 = 233.99 g/mole
= 233.99 g/mole
Molar mass of
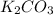 = 138.205 g/mole
= 138.205 g/mole
First we have to calculate the moles of
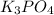 and
and
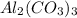
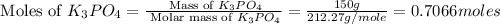

The given balanced reaction is,
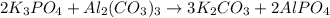
From the given reaction, we conclude that
2 moles of
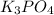 react with 1 mole of
react with 1 mole of
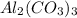
0.7066 moles of
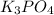 react with
react with
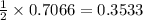 moles of
moles of
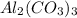
But the moles of
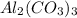 is, 0.3846 moles.
is, 0.3846 moles.
So,
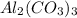 is an excess reagent and
is an excess reagent and
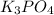 is a limiting reagent.
is a limiting reagent.
Now we have to calculate the moles of
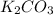 .
.
As, 2 moles of
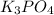 react to give 3 moles of
react to give 3 moles of
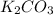
So, 0.7066 moles of
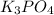 react to give
react to give
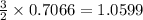 moles of
moles of
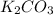
Now we have to calculate the mass of
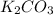 .
.
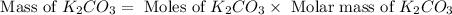
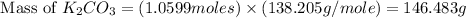
The theoretical yield of potassium carbonate = 146.483 g
The experimental yield of potassium carbonate = 125 g
Now we have to calculate the % yield of potassium carbonate.
Formula for percent yield :
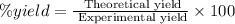
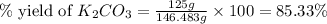
Therefore, the % yield of potassium carbonate is, 85.33%