Question

For some metal alloy, a true stress of 415 MPa produces a plastic true strain of 0.475. How much does a specimen of this material elongate when a true stress of 325 MPa is applied if the original length is 300 mm

Answer 1

`58.63\ \text{mm}`

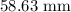
Step-by-step explanation:

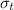`\sigma_t` = True stress = 415 MPa

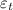`\varepsilon_t` = True strain = 0.475

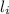`l_i` = Original length of the alloy = 300 mm

Let us assume n = Strain hardening component = 0.25

K = Constant

True stress is given by

`\sigma_t=K(\varepsilon_t)^n\\\Rightarrow K=(\sigma_t)/((\varepsilon_t)^n)\\\Rightarrow K=(415)/(0.475^(0.25))\\\Rightarrow K=499.89\approx 500\ \text{MPa}`

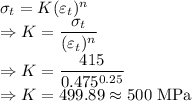
Now
`\sigma_t=325\ \text{MPa}`

`325=500(\varepsilon_t)^(0.25)\\\Rightarrow ((325)/(500))^{(1)/(0.25)}=(\varepsilon_t)\\\Rightarrow \varepsilon_t=0.1785`

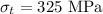
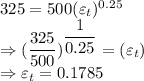
True strain is given by

`\varepsilon_t=\ln((l_f)/(l_i))\\\Rightarrow e^(\varepsilon_t)=(l_f)/(l_i)\\\Rightarrow l_f=l_ie^(\varepsilon_t)\\\Rightarrow l_f=300e^(0.1785)\\\Rightarrow l_f=358.63\ \text{mm}`

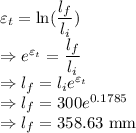
Elongation of material is
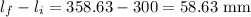`l_f-l_i=358.63-300=58.63\ \text{mm}`.