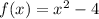Question

The graph of f(x) shown below has the same shape as the graph of g(x)= x^2 which of the following is the equation of f(x)

Answer 1

f(x)=x^2-4

Explanation:

So you know that the graph f(x)=x^2 has an origin at (0,0). The x coordinate of the minimum still is 0, but it has been shifted down 4, therefore:

f(x)=x^2-4

Answer 2

Option D -
`f(x)=x^2-4`

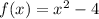
Explanation:

Given : The graph of
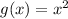`g(x)=x^2` and the graph of f(x) which is same shape as the graph of g(x).

To find : The equation of graph F(x)

Solution :

Since, According to the given statement we get f(x) by doing some changes in g(x).

In the graph, it seems that f(x) is shifting vertically downward by 4 unit than g(x).

When the function is shifted to vertically downward then

i.e, f(x) → f(x)-b ⇒ f(x) shifted downward by b unit.

`f(x)=x^2-4`

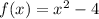
The graph of f(x) is in the direction of graph g(x).

Therefore, Option D is the correct.

The equation of graph f(x) is
`f(x)=x^2-4`