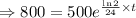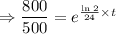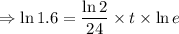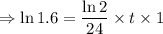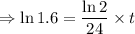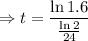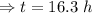The population of bacteria in a petri dish doubles every 24 h. The population of the bacteria is initially 500 organisms. How long will it take for the population of the bacteri…

Question

asked Jul 6, 2019 146k views

1 Answer

Naoto Usuyama · Answer 1 · 2019-07-10T04:02:58+0000

Answer:

C. 16.3

Explanation:

The function for exponential growth is,

y(t)=Ae^(rt)

where,

y(t) = the future amount,

A = initial amount,

r = rate of growth,

t = time.

As the population of bacteria in a Petri dish doubles every 24 h, so

$\Rightarrow 2A=Ae^(r* 24)$

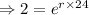
$\Rightarrow 2=e^(r* 24)$

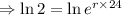
$\Rightarrow \ln 2=\ln e^(r* 24)$

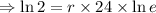
$\Rightarrow \ln 2={r* 24}* \ln e$

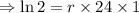
$\Rightarrow \ln 2={r* 24}* 1$

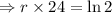
$\Rightarrow r* 24=\ln 2$

$\Rightarrow r=(\ln 2)/(24)$

The population of the bacteria is initially 500 organisms, so the function becomes,

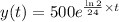
$y(t)=500e^{(\ln 2)/(24)* t}$

We have to calculate t, when the the population of bacteria becomes 800. So,

$\Rightarrow 800=500e^{(\ln 2)/(24)* t}$

$\Rightarrow (800)/(500)=e^{(\ln 2)/(24)* t}$

$\Rightarrow \ln (800)/(500)=\ln e^{(\ln 2)/(24)* t}$

$\Rightarrow \ln 1.6={(\ln 2)/(24)* t}* \ln e$

$\Rightarrow \ln 1.6={(\ln 2)/(24)* t}* 1$

$\Rightarrow \ln 1.6={(\ln 2)/(24)* t$

$\Rightarrow t=(\ln 1.6)/((\ln 2)/(24))$

$\Rightarrow t=16.3\ h$