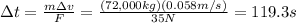Question

According to Newton's Third Law of Motion, small thruster rockets can be used to make fine adjustments in satellite orbits. One such rocket has a thrust of 35N. If it is fired to change the velocity of a 72,000 kg satellite by .058 m/s, how long should it be fired?

Answer 1

119.3 s

Step-by-step explanation:

The impulse given by the small rocket is equal to the change in momentum of the satellite:

`I=m\Delta v`

But the impulse can also be written as the product between the force applied by the rocket and the time, so:

`F\Delta t = m\Delta v`

where:

F = 35 N is the force applied by the small rocket

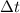`\Delta t` is the total time during which the force is applied

m = 72,000 kg is the mass of the satellite

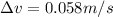`\Delta v = 0.058 m/s` is the change in velocity of the satellite

By substituting the numbers into the equation, we find
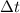`\Delta t`:

`\Delta t=(m\Delta v)/(F)=((72,000 kg)(0.058 m/s))/(35 N)=119.3 s`