Answer:
Given the equation:
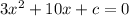
A quadratic equation is in the form:
 where a, b ,c are the coefficient and a≠0 then the solution is given by :
where a, b ,c are the coefficient and a≠0 then the solution is given by :
 ......[1]
......[1]
On comparing with given equation we get;
a =3 , b = 10
then, substitute these in equation [1] to solve for c;
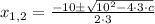
Simplify:
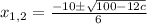
Also, it is given that the difference of two roots of the given equation is
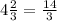
i.e,

Here,
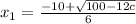 , ......[2]
, ......[2]
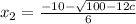 .....[3]
.....[3]
then;

simplify:
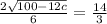
or
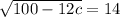
Squaring both sides we get;
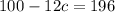
Subtract 100 from both sides, we get
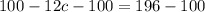
Simplify:
-12c = -96
Divide both sides by -12 we get;
c = 8
Substitute the value of c in equation [2] and [3]; to solve
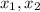
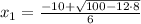
or
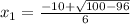 or
or
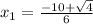
Simplify:

Now, to solve for
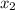 ;
;
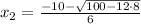
or
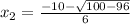 or
or
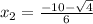
Simplify:

therefore, the solution for the given equation is:
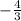 and -2.
and -2.