The age of painting was determined from the decay kinetics of the radioactive Carbon -14 present in the painting sample.
Given that the half life of Carbon-14 is 5730 years.
Radioactive decay reactions follow first order rate kinetics.
Calculating the decay constant from half life:
λ
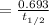
=
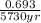 =
=
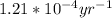
Setting up the radioactive rate equation:
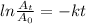
Where

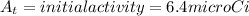
k = decay constant =
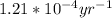
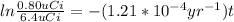
ln 0.125 =
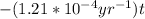
-2.079=
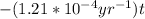
t=
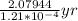
= 17185 years
t = 17185 years
Therefore age of the painting based in the radiocarbon -14 dating studies is 17185 years