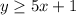Question

Write an inequality that describes the region of the coordinate plane not included in the graph of y<5x+1

Answer 1

An inequality which is not included in the graph of
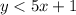`y < 5x+1` is:
`y\geq 5x+1`

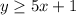
Explanation:

Given the inequality:
`y < 5x+1`

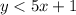
Since, the inequality divides the coordinate plane into 2 halves by a boundary line.

One side of the boundary line contains all solutions to the inequality and other sides of it does not contains the solution of that inequality.

For > and < : Boundary line is dashed

For ≥ and ≤ : Boundary line is solid.

Intercepts for the inequality are:

The related equation for the given inequality y =5x+1 ......[1]

x-intercepts:

Substitute y = 0 in equation [1] to solve for y:

0 = 5x+1 or

-1 = 5x

Simplify:

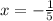`x = - (1)/(5)` = -0.2

x-intercepts is: (-0.2, 0).

y-intercepts:

Substitute x = 0 in equation [1] to solve for y:

y =5(0)+1

Simplify:

y= 1

y-intercepts is: (0 , 1).

Since, the solution is a region which is shaded for the given inequality and also the dashed line shows that the inequality does not include the line y= 5x +1 as shown below in the figure,

but the region which is not included in the graph of
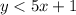`y < 5x+1` is:
`y\geq 5x+1`