Answer:
The unit rate of change is 9 units.
Explanation:
We have to draw a line which represents a proportional relationship between d and t. In the graph t is represented on x-axis represents and d is represent on y-axis.
It is given that increase of 0.2 units in t corresponds to an increase of 1.8 units in d.
The unit rate of change is also known as slope.
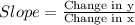
For the given case,
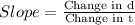
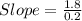
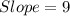
Therefore the unit rate of change is 9 units.
There is a proportional relationship between d and t, therefore the line must be passing through (0,0).
The point slope form of a line

Where m is the slope.
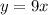
Therefore the equation of line is
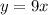 .
.