Answer:
Explanation:
It is given that in ΔABC,
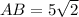 , ∠A=45°, ∠C=30°.
, ∠A=45°, ∠C=30°.
Now, using the angle sum property in ΔABC, we have
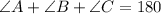
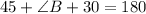
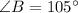
Using the sine law, we have
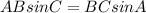
Substituting the given values, we have
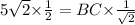
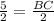
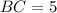
Again using sine law, we have

Substituting the values, we have

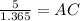

Therefore, the value of BC and AC are
 and
and
 .
.