[Note: you can only combine exponents when the base is the same.
x³ "x" is where the base is
For example:
x²(y³) = x²y³
When you multiply a variable/number with an exponent by a number with an exponent, you add the exponents together.
For example:
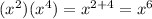
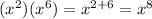
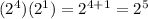
When an exponent is negative, you move the number and the exponent to the other side of the fraction to make the exponent positive.
For example:
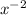 or
or
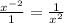
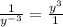 or y³
or y³
A.)
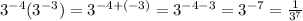
B.)
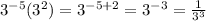
C.)
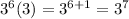
D.)
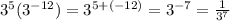
E.)
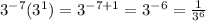
F.)
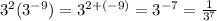
Your answer is A, D, F