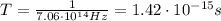Question

The wavelength of violet light is about 425 nm (1 nanometer = 1 × 10−9 m). what are the frequency and period of the light waves?

Answer 1

1) Frequency:
`7.06\cdot 10^(14) Hz`

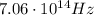
The frequency of electromagnetic radiation is given by:

`f=(c)/(\lambda)`

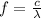
where

`c = 3 \cdot 10^8 m/s` is the speed of light

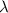`\lambda` is the wavelength

In this case, the wavelength of the radiation is

`\lambda=425 nm=425\cdot 10^(-9) m`

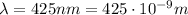
Therefore the frequency is

`f=(3\cdot 10^8 m/s)/(425 \cdot 10^(-9) m)=7.06\cdot 10^(14) Hz`

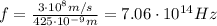
2) Period:
`1.42\cdot 10^(-15) s`

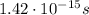
The period is equal to the reciprocal of the frequency of the wave:

`T=(1)/(f)`

Using the frequency we found previously,
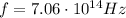`f=7.06\cdot 10^(14) Hz`, we find:

`T=(1)/(7.06\cdot 10^(14) Hz)=1.42\cdot 10^(-15) s`