Question

A hot bowl of soup cools according to Newton’s law of cooling. Its temperature (degrees F) at time t is given by T(t)=76+105e^(-0.125t), where t is given in minutes.

What was the initial temperature of the soup?


What is the temperature of the soup after 30 minutes?

Answer 1

a) T=181°F

b) T=78.469°F

Explanation:

In this case big T is temperature and little t is time in minutes, in physics this is usually the case.

Now for the initial temperature time is zero minutes so:

Let t=0

`T(0)=76+105e^(-0.125(0))\\\\T(0)=76+105=181`

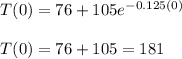
And so the initial temperature of the soup is 181°F.

The temperature after 30 minutes is:

Let t=30

`T(30)=76+105e^(-0.125(30))\\\\=76+105e^(-3.75)\\\\=78.469`

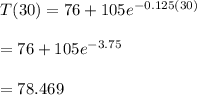
So the temperature after 30 minutes is 78.469°F. If you have a graphing calculator replace T(t) with y and t with x and look at when x=0 and x=30 your y will represent temperature.