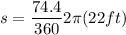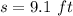1 Answer

Laures · Answer 1 · 2022-12-30T04:28:01+0000

Answer:

23.7°

9.1~ft

Explanation:

Formula for the area of a sector of central angle n (in degrees) and radius r:

$A = (n)/(360^\circ)\pi r^2$

We have:

A = 100 ft^2

r = 22 ft

We need to find:

r

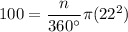
$100 = (n)/(360^\circ)\pi (22^2)$

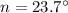
$n = 23.7^\circ$

The central angle measures 23.7°.

Formula for the length of an arcs of a circle with central angle n (in degrees) and radius r:

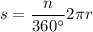
$s = (n)/(360^\circ)2 \pi r$

We have:

n = 23.7°

r = 22 ft

We need to find:

s

$s = (74.4)/(360)2 \pi (22 ft)$

s = 9.1~ft

Please log in or register to add a comment.