Question

A 15-ft ladder is leaning against a wall. If the top of the ladder slides down the wall at a rate of 0.33 ft/sec, how fast, in ft/sec, is the bottom of the ladder sliding away from the wall, at the instant when the bottom of the ladder is 9 ft from the wall? Answer with two decimal places.

Answer 1

Explanation:

Alright, lets get started.

Please refer the diagram I have attached.

The ladder is represented with red color and the length of the ladder is given as 15 feet.

When the bottom of the ladder is 9 feet from the wall, at that instant, the height of the ladder can be find by using Pythagorean theorem.

`x^2 + y^2 = L^2`

`9^2 + y^2 = 15^2`

`81 + y^2 = 225`

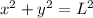
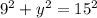
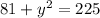
Subtracting 81 in both sides

`y^2 =225-81 = 144`

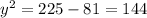
Taking square root of both sides

`y = 12`

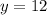
Now, we know

`x^2 + y^2 = 15^2`

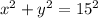
Differentiating with respect of t

`(d)/(dt)(x^2) +(d)/(dt)(y^2) = 0`

`2x(dx)/(dt) + 2y(dy)/(dt) = 0`

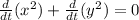
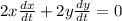
As per given in question, top of the ladder slides down the wall at the rate of 0.33 ft per second.

Downwards means its negative, so

Plugging the value of
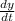`(dy)/(dt)` as -0.33

`2x(dx)/(dt) - 2y*0.33= 0`

`x(dx)/(dt) - y*0.33= 0`

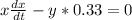
Plugging the value of x and y that we previously found

`9*(dx)/(dt)-12*0.33 = 0`

`9*(dx)/(dt)-3.96=0`

`9*(dx)/(dt)=3.96`

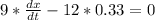
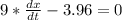
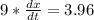
Dividing 9 in both sides

`(dx)/(dt)=(3.96)/(9)=0.44`

Hence the bottom of the ladder is sliding at 0.44 feet per second. : Answer

Hope it will help :)