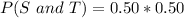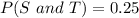Question

Genes S and T are not linked. If there is a 50% probability that allele S is in a gamete and there is a 50% probability that allele T is in a gamete, what is the probability that both are in the same gamete

Answer 1

The probability that both are in the same gamete is 0.25

Explanation:

Given

`P(S) = 50\%`

`P(T) = 50\%`

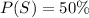
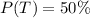
Required

Determine the probability that both are in same gamete

The required probability means: P(S and T)

This is then calculated as:

`P(S\ and\ T) = P(S) * P(T)`

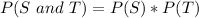
Substitute values for P(S) and P(T)

`P(S\ and\ T) =50\% * 50\%`

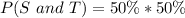
Convert to decimal

`P(S\ and\ T) =0.50* 0.50`

`P(S\ and\ T) =0.25`