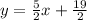Question

Stuck Please help...... 1,2,5,6

Answer 1

Slope-intercept form:

y = mx + b "m" is the slope, "b" is the y-intercept

For lines to be parallel, they have to have the SAME slope.

1.) The given line's slope is -7/5, so the parallel line's slope is also -7/5

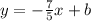`y=-(7)/(5)x+b` Plug in (2, -3) to find "b"

`-3 = -(7)/(5)(2)+b`

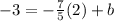
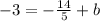`-3=-(14)/(5)+b` Add 14/5 on both sides

`-3+(14)/(5)=b` Make the denominators the same

`(-15)/(5)+(14)/(5) =b\\-(1)/(5)=b`

`y=-(7)/(5)x-(1)/(5)`

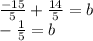
2.) The given line's slope is 1/2, so the parallel line's slope is also 1/2

y = 1/2x + b Plug in (4,5) to find "b"

5 =
`(1)/(2)`(4) + b

5 = 2 + b

3 = b

`y=(1)/(2) x+3`

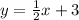
5.) The given line's slope is -2/5, so the parallel line's slope is also -2/5

y = -2/5x + b Plug in (-5, -4)

-4 = -2/5(-5) + b

-4 = 2 + b

-6 = b

`y=-(2)/(5)x-6`

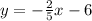
6.) -5x + 2y = 6 Isolate "y", add 5x on both sides

2y = 6 + 5x Divide 2 on both sides

y = 3 + 5/2x

The slope is 5/2, so the parallel line's slope is also 5/2

y = 5/2x + b Plug in (-3,2)

2 = 5/2(-3) + b

2 = -15/2 + b Add 15/2 on both sides

2 + 15/2 = b Make the denominator the same

4/2 + 15/2 = b

19/2 = b

`y=(5)/(2)x+(19)/(2)`