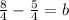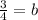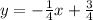Slope-intercept form:
y = mx + b "m" is the slope, "b" is the y-intercept
For lines to be perpendicular, their slopes have to be the opposite/negative reciprocals (flipped sign and number)
For example:
slope is 2
perpendicular line's slope is -1/2
slope is -2/3
perpendicular line's slope is 3/2
3.) y = 2x - 2
The given line's slope is 2, so the perpendicular line's slope is -1/2
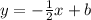 To find "b", plug in the point (-5 , 5) into the equation
To find "b", plug in the point (-5 , 5) into the equation
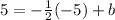
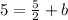 Subtract 5/2 on both sides
Subtract 5/2 on both sides
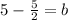 Make the denominators the same
Make the denominators the same
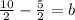
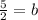
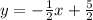
4.) -6x + 5y = -10 Get "y" by itself, add 6x on both sides
5y = -10 + 6x Divide 5 on both sides
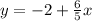
The given line's slope is 6/5, so the perpendicular line's slope is -5/6.
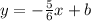 Plug in (-2, 5)
Plug in (-2, 5)
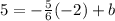
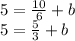 Subtract 5/3 on both sides
Subtract 5/3 on both sides
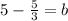 Make the denominators the same
Make the denominators the same
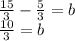
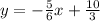
7.) Perpendicular line's slope is -2
y = -2x + b Plug in (1,4)
4 = -2(1) + b
4 = -2 + b
6 = b
y = -2x + 6
8.) Perpendicular line's slope is -1/4
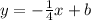 Plug in (-5 , 2)
Plug in (-5 , 2)
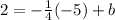
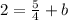 Subtract 5/4 on both sides
Subtract 5/4 on both sides
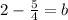 Make the denominators the same
Make the denominators the same