Question

Find the inverse of each given functions h(x)=2x-4/3

Answer 1

h^-1(x) = (3x+4)/2

answer choice c

Answer 2

`h(x')=(x)/(2) +(2)/(3)`

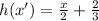
Explanation:

We are given the following function:

`h(x)=2x-(4)/(3)`

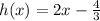
To find the inverse of this function, we will put this function equal to y (another variable) and then make x the subject of it.

`y=2x-(4)/(3)`

`y+(4)/(3) =2x`

`(y)/(2) +(4)/(6) =x`

`x=(y)/(2) +(2)/(3)`

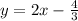
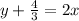
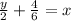
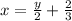
Now changing back the variable y to x to make it the inverse of h(x) to get:

`h(x')=(x)/(2) +(2)/(3)`

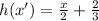
Therefore, the inverse of the given function h(x) is
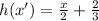`h(x')=(x)/(2) +(2)/(3)`.