Question

If 23/8, 11/2, 9/6, and 15/7 are placed in order from least to greatest, which would be first?

Answer 1

`(9)/(6)`

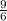
Explanation:

The given fractions are;

`(23)/(8),(11)/(2),(9)/(6),(15)/(7)`

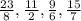
The least common denominator is
`168`.

We express all the fractions in equivalent form with the LCD as the denominator.

`(23)/(8)=(21*23)/(21*8)=(483)/(168)`

`(11)/(2)=(84*11)/(84*2)=(924)/(168)`

`(9)/(6)=(28*9)/(28*6)=(252)/(168)`

`(15)/(7)=(24*15)/(24*7)=(360)/(168)`

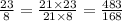
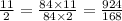
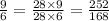
We now compare the equivalent forms and arrange from the least to the greatest.

`(252)/(168)\:<\:(360)/(168)\:<\:(483)/(168)\:<\:(924)/(168)`

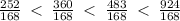
This implies that,

`(9)/(6)\:<\:(15)/(7)\:<\:(23)/(8)\:<\:(11)/(2)`

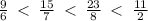
Therefore the first would be
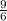`(9)/(6)`.