Question

A random sample of 70 printers discovered that 25 of them were being used in small businesses. find the 95% limit for the population proportion of printers that are used in small businesses.

Answer 1

The sample proportion of printers used in small business is:

`\hat{p}=(25)/(70)=0.3571`

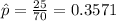
The 95% confidence interval for the population proportion of printers that are used in small businesses is:

`\hat{p} \pm z_{(0.05)/(2)} \sqrt{\frac{\hat{p}(1-\hat{p})}{n} }`

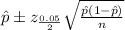
Where:

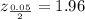`z_{(0.05)/(2)}=1.96` is the critical value at 0.05 significance level

`\therefore 0.3571 \pm 1.96 \sqrt{(0.3571(1-0.3571))/(70) }`

`0.3571 \pm 0.1122`

`\left ( 0.3571 - 0.1122, 0.3571 + 0.1122 \right)`

`\left(0.245,0.469 \right)`

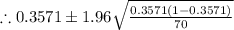
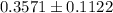
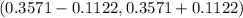
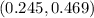
Therefore, the 95% confidence interval for the population proportion of printers that are used in small businesses is (0.245 , 0.469)