Question

Give an example of an infinite non abelian group that has exactly six elements of finite order

Answer 1

`<a, b, c, d, e, f | a^2 = b^2 = c^2 = d^2 = e^2 = f^2 = 1>`

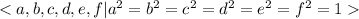
Explanation:

An infinite non-abelian group that has exactly six elements of finite order is,

`<a, b, c, d, e, f | a^2 = b^2 = c^2 = d^2 = e^2 = f^2 = 1>`

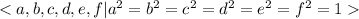
Multiplication by concatenation can be done, for example,

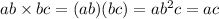`ab * bc = (ab)(bc) = a b^2 c = ac`, since
`b^2 = 1`.

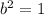This group is non-commutative, because
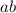`ab` is not equal to
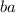`ba` (as this is not a relation in the given presentation).

Now, this is infinite, because we can have 'words' of
`a, b, c, d, e, f` of any length (the only simplifications we can use is when
`a^2, b^2, c^2, d^2, e^2, f^2` show up).

Therefore, any word (not containing
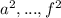`a^2, ..., f^2`) containing more than one of
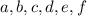`a,b,c,d,e,f` must have infinite order.