Essentially, we are trying to find the missing constant term of
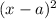 (remember that we are subtracting
(remember that we are subtracting
 due to the negative sign in front of the second term). Let's expand this to see what we can work with:
due to the negative sign in front of the second term). Let's expand this to see what we can work with:
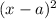
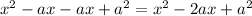
Now, we know the second term is
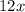 , so let's set the second term in the polynomial we just found equal to
, so let's set the second term in the polynomial we just found equal to
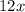 :
:
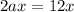

- Divide both sides of the equation by

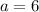
- Divide both sides of the equation by 2
We have found
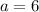 . We know the missing constant term is
. We know the missing constant term is
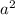 , according to the polynomial we found earlier. Thus, the missing term is:
, according to the polynomial we found earlier. Thus, the missing term is:

The missing constant term is 36.