Question

Write an equation for a line that is parallel to the given line that passes through the given point. Explain how you found the equation. y=2x+7;(3,11) Show all work plz

Answer 1

First, remember that if two lines are parallel, they have the same slope. The problem already gave us a point on the line and we now have the power to find the slope. Since we have the slope and a point on the line, we are going to find the equation of the line through the point-slope formula, which is:

`(y - y_1) = m(x - x_1)`

• 
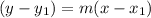
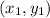  `(x_1, y_1)` is a point on the line
• 
  `m` is the slope of the line

The equation given to us has a slope of 2, as we can see because the line is in slope-intercept form. Also, we are given the point (3, 11), which we are told is on the line. Since we are already given all of the information for the point-slope formula, we can simply substitute it in and solve for the equation.

`(y - 11) = 2(x - 3)`

• Set up

`y - 11 = 2x - 6`

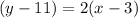
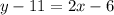
• Use the Distributive Property on both sides

`y = 2x + 5`

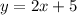
• Add 11 to both sides and simplify

The equation of our line is y = 2x + 5.

Answer 2

Slope-intercept form:

y = mx + b "m" is the slope, "b" is the y-intercept (the y value when x = 0)

For lines to be parallel, they have to have the SAME slope.

The given line's slope is 2, so the parallel line's slope is also 2.

y = 2x + b

To find "b", plug in the point (3,11) into the equation.

y = 2x + b

11 = 2(3) + b Multiply 2 and 3

11 = 6 + b Subtract 6 on both sides

5 = b

y = 2x + 5