Based on the picture, we can say that ∠FDE and ∠EDC are supplementary angles, meaning they add to 180°. Thus, we can sum up the measues of those angles to 180 and solve for
 :
:
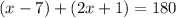
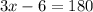
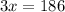
- Add 6 to both sides of the equation
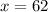
- Divide both sides of the equation by 3
We have now found that
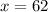 . However, we are looking to find ∠ADC, which doesn't have any indication of measurement. However, we can see that ∠ADC and ∠FDE are vertical angles, meaning that they have the same measurement. Let's use the fact that
. However, we are looking to find ∠ADC, which doesn't have any indication of measurement. However, we can see that ∠ADC and ∠FDE are vertical angles, meaning that they have the same measurement. Let's use the fact that
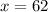 to find ∠FDE first.
to find ∠FDE first.
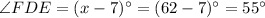
We have found that ∠FDE is 55°. Thus, the measure of ∠ADC is 55°.