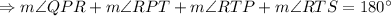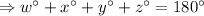Question

Help please thank you (next)

Answer 1

`\boxed{\boxed{w^(\circ)+x^(\circ)+y^(\circ)+z^(\circ)=180^(\circ)}}`

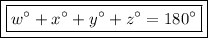
Explanation:

Given that PQST is a parallelogram, so

`\Rightarrow QS\ ||\ PT`

As a parallelogram is a quadrilateral with both pairs of opposite sides parallel.

PR and RT are the transversal to the parallel lines QS and PT, so

`\Rightarrow m\angle QRP=m\angle RPT\ and\ m\angle SRT=m\angle RTP`

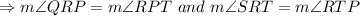
As they are alternate interior angles.

Hence,

`\Rightarrow m\angle RPT=x^(\circ)\ and\ m\angle RTP=y^(\circ)`

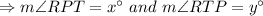
When the two lines being crossed are parallel lines the consecutive interior angles add up to 180°.

So,
`m\angle QPT+m\angle STP=180^(\circ)`

`\Rightarrow m\angle QPR+m\angle RPT+m\angle RTP+m\angle RTS=180^(\circ)`

`\Rightarrow w^(\circ)+x^(\circ)+y^(\circ)+z^(\circ)=180^(\circ)`