Question

If the measure of one side of a square is increased by 2 centimeters and the measure of the adjacent side is decreased by 2 centimeters, the area of the resulting rectangle is 32 square centimeters. Find the measure of one side of the square.

Answer 1

8cm

Explanation:

1. 32/4=8

So each side must equal 8.

Answer 2

One of the sides is approximately 3 centimeters.

Explanation:

We know that a square has equivalent sides, which we are gonna call
`x`.

If one side increases by 2 centimeters, this can be represented as

`x+2`

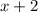
If the adjacent side decreases by 2 centimeters, its representation is

`x-2`

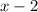
So, the area of the new figure is

`A=(x+2)(x-2)`

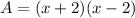
Which, according to the problem, equals 32 square centimeters.

`(x+2)(x-2)=32`

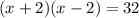
Let's solve this equation, first we need to apply the distributive property

`(x+2)(x-2)=32\\x^(2) -2x+2x+4=32\\x^(2) +4=32\\x^(2) =32-4=28\\x=√(28)\\ x \approx 5`

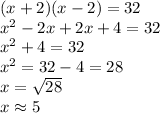
We replace this in one of the sides expressions

`x-2=5-2=3`

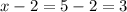
Therefore, one of the sides is approximately 3 centimeters.