Answrer
Find out the what is the perimeter of the rectangle .
To prove
Now as shown in the figure.
Name the coordinates as.
A(−3, 4) ,B (7, 2) , C(6, −3) , and D(−4, −1) .
In rectangle opposite sides are equal.
Thus
AB = DC
AD = BC
Formula
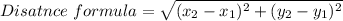
Now the points A(−3, 4) and B(7, 2)
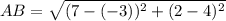
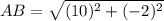
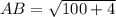
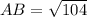
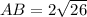
Thus
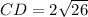
Now the points
A (−3, 4) , D (−4, −1)
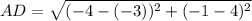
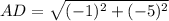
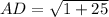
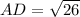
Thus
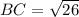
Formula
Perimeter of rectangle = 2 (Length + Breadth)
Here
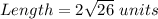
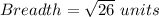
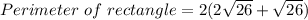
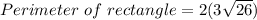
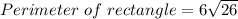
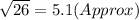
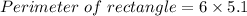
Perimeter of a rectangle = 30.6 units.
Therefore the perimeter of a rectangle is 30.6 units.