Question

The coordinates of the vertices of a rectangle are (−3, 4) , (7, 2) , (6, −3) , and (−4, −1) . What is the perimeter of the rectangle? Round each step to the nearest tenth. Enter your answer as a decimal in the box.

Answer 1

Answrer

Find out the what is the perimeter of the rectangle .

To prove

Now as shown in the figure.

Name the coordinates as.

A(−3, 4) ,B (7, 2) , C(6, −3) , and D(−4, −1) .

In rectangle opposite sides are equal.

Thus

AB = DC

AD = BC

Formula

`Disatnce\ formula = \sqrt{(x_(2) - x_(1))^(2) +(y_(2) - y_(1))^(2)}`

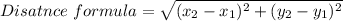
Now the points A(−3, 4) and B(7, 2)

`AB = \sqrt{(7- (-3))^(2) +(2- 4)^(2)}`

`AB = \sqrt{(10)^(2) +(-2)^(2)}`

`AB = √(100+4)`

`AB = √(104)`

`AB = 2√(26)\units`

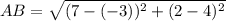
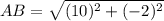
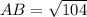
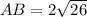
Thus

`CD= 2√(26)\units`

Now the points

A (−3, 4) , D (−4, −1)

`AD = \sqrt{(-4 - (-3))^(2) +(-1- 4)^(2)}`

`AD = \sqrt{(-1)^(2) +(-5)^(2)}`

`AD = √(1 + 25)`

`AD = √(26)\units`

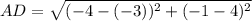
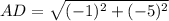
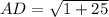
Thus

`BC = √(26)\units`

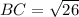
Formula

Perimeter of rectangle = 2 (Length + Breadth)

Here

`Length = 2√(26)\ units`

`Breadth = √(26)\ units`

`Perimeter\ of\ rectangle = 2(2√(26) +√(26))`

`Perimeter\ of\ rectangle = 2(3√(26))`

`Perimeter\ of\ rectangle = 6√(26)`

`√(26) = 5.1 (Approx)`

`Perimeter\ of\ rectangle = 6* 5.1`

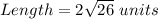
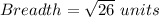
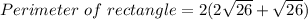
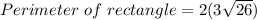
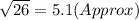
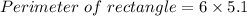
Perimeter of a rectangle = 30.6 units.

Therefore the perimeter of a rectangle is 30.6 units.