Answer:
The correct option is D.
Explanation:
The given inequality is
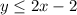
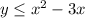
Any point is a solution of this system of inequality if it satisfy both inequalities.
Check the inequalities by each option.
For (-2,-1),
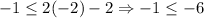
This statement is false, because -1 is greater than -6. Therefore (-2,-1) is not a solution and option A is incorrect.
For (1,3),
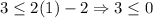
This statement is false, because 3 is greater than 0. Therefore (1,3) is not a solution and option B is incorrect.
For (2,1),
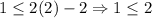

This statement is false, because 1 is greater than -2. Therefore (2,1) is not a solution and option C is incorrect.
For (4,2),
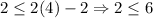
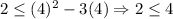
Both statements are true. Therefore (4,2) is a solution and option D is correct.