Answer:
−1 + i times the square root of 3
is the answer.
Explanation:
Given is a quadratic equation in x
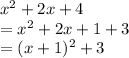
using completion of squares method
Equate to 0
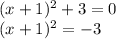
Take square root
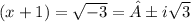
Subtract one from both sides
x = [/tex]-1±i\sqrt{3}[/tex]
The last option namely
−1 + i times the square root of 3 only matches with our answre
Hence last option is right.