Question

What is the equation of the quadratic graph with a focus of (3, 1) and a directrix of y = 5?

f(x) = one eighth (x − 3)2 + 3
f(x) = −one eighth (x − 3)2 + 3
f(x) = one eighth (x − 3)2 − 3
f(x) = −one eighth (x − 3)2 − 3

Answer 1

`f(x)=-(1)/(8)(x-3)^2+3`

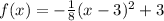
Explanation:

We want to find the equation of the parabola with a focus of
`(3,1)` and directrix
`y=5`.

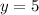Considering the directrix, the quadratic graph must open downwards.

The equation of this parabola is given by the formula,

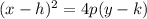`(x-h)^2=4p(y-k)`, where
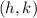`(h,k)` is the vertex of the parabola.

The axis of this parabola meets the directrix at
`(3,5)`.

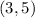Since the vertex is the midpoint of the focus and the point of intersection of the axis of the parabola and the directrix,

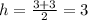`h=(3+3)/(2)=3` and
`k=(5+1)/(2)=3`.

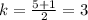The equation of the parabola now becomes,

`(x-3)^2=4p(y-3)`.

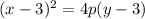Also
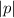`|p|` is the distance between the vertex and the directrix.

`|p|=2`

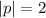
This implies that
`p=-2\:or\:2`.

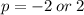Since the parabola turns downwards,

`p=-2`.

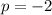Our equation now becomes,

`(x-3)^2=4(-2)(y-3)`.

`(x-3)^2=-8(y-3)`.

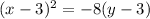We make y the subject to get,

`y=-(1)/(8)(x-3)^2+3)`.

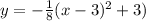This is the same as

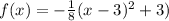`f(x)=-(1)/(8)(x-3)^2+3)`.