Question

Given the function f(x)=2/(x+4)^2 determine the intervals where the function is positive, negative,zero and undefined

Answer 1

The correct answer is B.

Explanation:

Edg. 2021

The answer above is incorrect.

Answer 2

The function is positive at
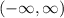`(-\infty,\infty)`. The function has no zeros. The function is undefined at x= -4.

Explanation:

The given function is

`f(x)=(2)/((x+4)^2)`

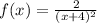
It is rational function. The numerator is constant and the degree of denominator function is 2, therefore the value of denominator is always positive for any value of x.

Therefore the function is positive for any real value of x. The function is positive at
`(-\infty,\infty)`.

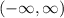To find the zeros we have to equate numerator equal to 0.

`2=0`

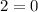
Since this statement is false for all values of x, therefore the function has no zeros.

Equate denominator equal to 0.

`(x+4)^2=0`

`x+4=0`

`x=-4`

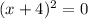
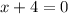
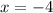
The number -4 divides the number line into two parts
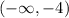`(-\infty,-4)` and
`(-4,\infty)`.

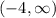Since at x=-4 the value of the denominator is equal to 0 and the function is not defined.