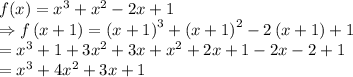Answer:
Option B is correct
Step-by-step explanation:
Given:
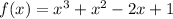
If a graph
 is shifted a units to the left then it becomes
is shifted a units to the left then it becomes
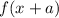
Here, the graph is shifted 1 unit to the left . On taking a=1, we get graph
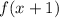
Using formula
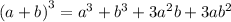 , we get
, we get
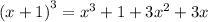
Using formula
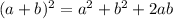 , we get
, we get
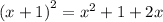
Using distributive property over multiplication i.e
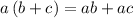 , we get
, we get

Therefore,