Answer:
1)
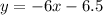
2)
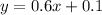
3)
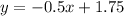
Step-by-step explanation:
Since we know that the segment joining the mid-points of two sides of a triangle is known as mid-segment of triangle. A triangle has three mid-segments.
1) Let us find midpoints of side ED and DF using midpoint formula.
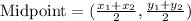
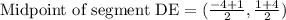
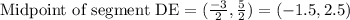
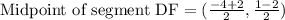
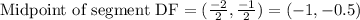
Now let us find slope of line joining points (-1.5,2.5) and (-1,-0.5) using slope formula.

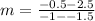
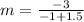
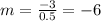
Now let us substitute our values in slope intercept form of the line to find y-intercept.
 , where m= slope of the line, b= y-intercept.
, where m= slope of the line, b= y-intercept.
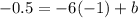
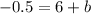
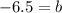
Upon substituting m=-6 and b= -6.5 in slope intercept form of line, we will get,
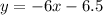
Therefore, 1st equation that represents the mid-segment parallel to side EF of the given triangle will be
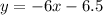 .
.
2) Let us find midpoint of segment EF.

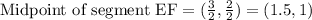
Now let us find the slope of the line passing through points (1.5,1) and (-1,-0.5).
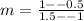
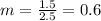
Now let us find y-intercept of line parallel to segment DE.
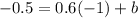


Upon substituting m=0.6 and b=0.1 in slope intercept form of line we will get,
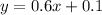
Therefore, second equation that represents the mid-segment parallel to side DE of the given triangle will be
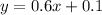 .
.
3) Now let us find the slope of the mid-segment joining mid-points of segment DE and EF that are (-1.5,2.5) and (1.5,1).
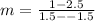
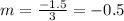
Now let us find y-intercept of our line.

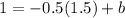
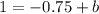
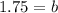
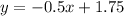
Therefore, the third equation that represents the mid-segment parallel to side DF of the given triangle will be
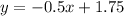 .
.