Question

If sin Θ=-3/5 and the angle is in quadrant IV, what is cot Θ?

-3/4
3/4
4/3
-4/3

Answer 1

ANSWER


`\cot( \theta) = - (4)/(3)`


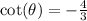
Step-by-step explanation

We were given that


`\sin( \theta) = - (3)/(5)`

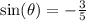
We need to find

`\cot( \theta) .`

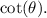
We know that,


`\cot( \theta) = ( \cos( \theta) )/( \sin( \theta) )`


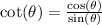
We now need to find

`\cos( \theta)`

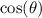
using the Pythagorean identity or the right angle triangle.

According to the Pythagorean identity,


`\cos^(2) \theta + \sin^(2) \theta = 1`



`\cos^(2) \theta + {( ( - 3)/(5) )}^(2) = 1`




`\cos^(2) \theta + (9)/(25) = 1`



`\cos^(2) \theta = 1 - (9)/(25)`


`\cos^(2) \theta = (16)/(25)`





`\cos\theta = \pm \: \sqrt{ (16)/(25) }`



`\cos\theta = \pm \: (4)/(5)`

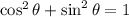
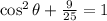
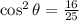
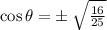
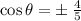
Since we are dealing with the fourth quadrant,


`\cos\theta = (4)/(5)`


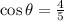
This implies that,



`\cot( \theta) = ( (4)/(5) )/( - (3)/(5) )`


`\cot( \theta) = - (4)/(3)`

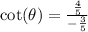
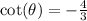
The correct answer is D.