Answer:
The equation of the parallel line is: y = -1/2x + 12
Explanation:
The slope-intercept form of the line equation
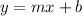
where
Given the line
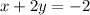
writing into the slope-intercept form
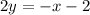
dividing both sides by 2
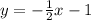
comparing with the slope-intercept form y = mx+b
Thus, the slope m of the equation is: m = -1/2
We know that the parallel lines have the same slope.
Thus, the slope of a new line parallel to x + 2y = -2 is also: -1/2
Given that the line intersects the point (6, 9).
so substituting m = -1/2 and (6, 9) in the slope-intercept form to determine the y-intercept
y = mx+b
9 = -1/2(6) + b
9 = -3 + b
b = 9+3
b = 12
Thus, the y-intercept b = 12
now substituting b = 12 and m = -1/2 in the slope-intercept
y = mx+b
y = -1/2x + 12
Therefore, the equation of the parallel line is: y = -1/2x + 12