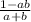Solve for x: 1/abx = 1/a + 1/b + 1/x

Question

asked Feb 10, 2019 69.7k views

1 Answer

Jhuang · Answer 1 · 2019-02-15T15:20:49+0000

Answer:

Value of
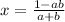
x = (1-ab)/(a+b)

Explanation:

Given that:
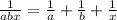
(1)/(abx) = (1)/(a) +(1)/(b) +(1)/(x)

Solve for x;

Taking LCM of a , b and x is abx.

(1)/(abx) =(bx+ax+ab)/(abx)

Multiply both sides by abx we get;

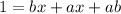
1 = bx+ax+ab

Subtract ab from both sides we get;

1-ab = bx + ax

Using distributive property:
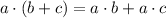
$a\cdot (b+c) = a\cdot b +a \cdot c$

1- ab = x(a + b)

Divide both sides by a+b we get;

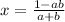
x = (1-ab)/(a+b)

Therefore, value of x is;