Answer:
600m/s
Explanation:
Step 1
First step is to use declare variables for Bill's and Susan's cruising speed.Let
 the speed of Susan's plane. This implies that Bill's plane is
the speed of Susan's plane. This implies that Bill's plane is
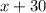
Step 2
To calculate the time traveled given distance and speed we use the formula
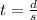 where
where
 is speed,
is speed,
 is the distance,
is the distance,
 is the time.
is the time.
The time taken by Bill's plane is
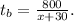
The time taken by Susan's plane is

Step 3
Since the time taken by both planes is the same, we solve for Susan's speed as shown below,
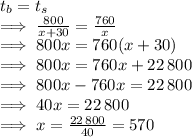
Step 4
Since Susan's plane travels at a speed of 570mph, we can inder that Bill's plane travels at a speed of (570+30)mph=600mph.