Question

Solve the following quadratics. State the FACTORS AND SOLUTIONS. 1. 2x^2 - 7x + 3 2. 3x^2 + 7x +2

Answer 1

1. x = 3, 1/2 (solutions); (x - 3)(2x - 1) (factors)

2. x = -1/3, -2 (solutions); (3x + 1)(x + 2) (factors)

Explanation:

1. 2x^2 - 7x + 3

To solve problem 1, you will need to identify your a, b, and c values in this quadratic function.

Since this problem is in standard form, it will be easy to identify these values. The standard form of a quadratic function is ax^2 + bx + c.

The a value is 2, the b value is -7, and the c value is 3 if we use our standard form and see which numbers are plugged into it.

Since we know that

• a = 2
• b = -7
• c = 3

we can use the quadratic formula:
`x = (-b~\pm~√(b^2~-~4ac) )/(2a)`

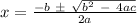
Substitute the a, b, and c values into the quadratic formula:
`x=(-(-7)\pm√((-7)^2-4(2)(3)) )/(2(2))`

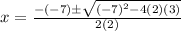
Now simplify using the laws of pemdas:
`x=(7\pm√((49)-(24)) )/(4)`

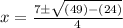
Simplify even further:
`x=(7\pm√((25)) )/(4) \rightarrow x=(7\pm (5) )/(4)`

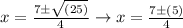
Now split this equation into two equations to solve for x:
`x=(12 )/(4) ~~and~~ x=(2 )/(4)`

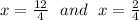
12/4 can be simplified to 3, and 2/4 can be simplified to 1/2.

This means your solutions to problem 1 is 3, 1/2.

`\boxed {x=3,(1)/(2) }`

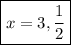
There is also another way to solve for the quadratic functions, and this was by factoring.

If you factor 2x^2 - 7x + 3 using the bottoms-up method, you will get (x - 3)(2x - 1).

After factoring, solving for the solutions is simple because all you have to do is set each factor to 0.

• x - 3 = 0
• 2x - 1 = 0

After solving for x by adding 3 to both sides, or by adding 1 to both sides then dividing by 2, you will end up with the same solutions: x = 3 and x = 1/2.

2. 3x^2 + 7x + 2

To save time I'll be using the bottoms-up factoring method, but remember to refer back to problem 1 (quadratic formula) if you prefer that method.

Factor this quadratic function using the bottoms-up method. After factoring you will have (3x + 1)(x + 2). These are your factors.

Now to solve for x and find the solutions of the quadratic function, you will set both factors equal to 0.

• 3x + 1 = 0
• x + 2 = 0

Solve.

First factor: 3x + 1 = 0

Subtract 1 from both sides.

3x = -1

Divide both sides by 3.

x = -1/3

Second factor: x + 2 = 0

Subtract 2 from both sides.

x = -2

Your solutions are x = -1/3 and x = -2.

`\boxed {x = -(1)/(3) , -2}`