Answer:
The roots of the of the function are 2,3 and 4.
Explanation:
The given function is
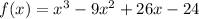
It is given that x=2 is a root of the function. So (x-2) is a factor of f(x).
According to the remainder theorem if a function is divided by (x-c), then the remainder is equal to f(c). If f(c) is equal to 0, therefore c is the root of the function.
Use synthetic method to divide f(x) by (x-2).
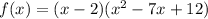

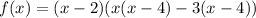
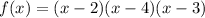
To find the roots equation the function equate the function equal to 0.
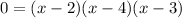
Equate each factor equal to 0.

Therefore the roots of the function are 2,3 and 4.