Question

In a small chess tournament, 20 matches were played. Find out how many people were involved if it is known that each participant played 2 games with every other participant in the tournament.

Answer 1

5 people

Explanation:

Answer 2

5

Explanation:

We are given that 20 matches were played in a small chess tournament.

We are also given that Each participant played 2 games with every other participant in the tournament.

We are required to find out how many people were involved in the game.

So, First Let no. of players involved be n

Since we are given for every match there should be two players out of n

Thus, number of ways they can play a match :
`^nC_2`

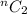
Since we know that each participant played 2 games with every other participant.

Thus , The total no. of games played =
`2 * ^nC_2`

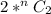
We can see that 20 matches were played in total

⇒
`2 * ^nC_2 = 20`

⇒
`^nC_2=(20)/(2)`

⇒
`^nC_2=10`

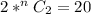
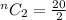
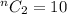
Thus using the combination formula i.e.
`(n!)/(r! * (n-r)!)`

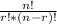
Since total players = n and r = 2

⇒
`(n!)/(2! * (n-2)!)=10`

⇒
`(n*(n-1)*(n-2)!)/(2! * (n-2)!)=10`

⇒
`(n*(n-1))/(2*1)=10`

⇒
`n*(n-1)=10*2`

⇒
`n*(n-1)=20`

⇒
`n*(n-1)-20=0`

⇒
`n^(2)-n-20=0`

⇒
`n^(2)-5n+4n-20=0`

⇒
`n(n-5)+4(n-25)=0`

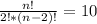
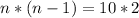
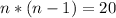
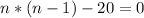
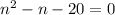
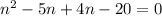
⇒(n+4)=0 , (n-5)=0

⇒ n = -4, 5

Number of players cannot be negative so neglect n = -4

Thus , Number of players involved were 5