Question

Which equation represents a parabola that opens upward has a minimum at x=3 and has a line of symmetry at x=3

Answer 1

A. y = x^2 -6x + 13

Explanation:

Answer 2

`y=x^2-6x+5`

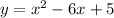
Explanation:

Let us consider the equation
`y=x^2-6x+5`

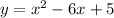
For a quadratic equation in a standard form,
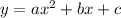`y=ax^2+bx+c`, the axis of symmetry is the vertical line
`x = (-b)/(2a)`.

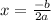Here in this case we have,
`a=1, b=-6 , c =5`

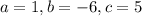
Putting the values we get,

`x = (-(-6))/(2* 1) = (6)/(2) =3`

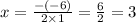
We can see that the axis of symmetry is x=3 and the graph is giving minimum at x=3.

Therefore, the required equation is
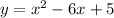`y=x^2-6x+5`. Refer the image attached.