Question

Which equations represent exponential growth?

Which equations represent exponential decay?

Answer 1

I took the quiz :)

Explanation:

Answer 2

Exponential growth:

2.
`P=4500(1.04)^(t)`

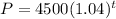
3.
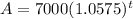
`A=7000(1.0575)^(t)`

5.
`P=45(2)^(t)`

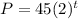
Exponential decay:

1.
`V=18000(0.78)^(t)`

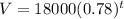
4.
`P=50((1)/(2))^(t)`

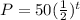
6.
`A=9000(0.9)^(t)`

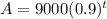
Explanation:

Since we know that an exponential function is in form
`y=a\cdot b^(x)` where a is initial value of function, b is exponential growth or decay. For exponential growth b should be greater than 1 and for exponential decay b should be less than 1

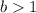`b>1` = Exponential growth.

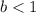`b<1` = Exponential decay.

Now let us look at our given equations one by one to determine which one is for exponential growth and which one is for exponential decay.

1.
`V=18000(0.78)^(t)`

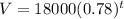
In this option a equals 18000 and b equals to 0.78. 0.78 is less than 1, therefore, this equation is representing exponential decay.

2.
`P=4500(1.04)^(t)`

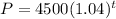
We can see that a equals 4,500 and b equals 1.04 and 1.04 is clearly greater than 1 , therefore, this equation is representing exponential growth.

3.
`A=7000(1.0575)^(t)`

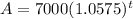
We can see that a equals 7000 and b equals 1.0575 and 1.0575 is clearly greater than 1 , therefore, this equation is representing exponential growth.

4.
`P=50((1)/(2))^(t)`

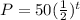
We can see that a equals 50 and b equals 1/2 and 1/2 (0.5) is clearly less than 1, therefore, this equation is representing exponential decay.

5.
`P=45(2)^(t)`

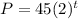
We can see that a equals 45 and b equals 2 and 2 is clearly greater than 1 , therefore, this equation is representing exponential growth.

6.
`A=9000(0.9)^(t)`

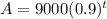
We can see that a equals 9000 and b equals 0.9 and 0.9 is clearly less than 1 , therefore, this equation is representing exponential decay.