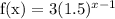Question

Someone help!!!! Plzz

Answer 1

`\text{C. f(x)} = 3(1.5)^(x-1)`

Explanation:

The numbers don’t increase by a constant amount, so this is not an arithmetic sequence.

It appears to be a geometric sequence.

The general formula for each term in a geometric sequence is

aₙ = a₁rⁿ⁻¹

===============

Calculate the value of r

You can calculate the r-value by dividing any two consecutive terms in the sequence.

rₙ = aₙ/aₙ₋₁

a₂/a₁ = 4.5/3 = 1.5

a₃/a₂ = 6.75/4.5 = 1.5

a₄/a₃ = 10.125/6.75 = 1.5

a₅/a₄ = 15.1875/10.125 = 1.5

r = 1.5

===============

Determine the formula for the nth term

a₁ = 3; r = 1.5 Substitute the values

aₙ = 3(1.5)ⁿ⁻¹ Write the equation as a function of x

`\text{f(x)} = 3(1.5)^(x-1)`