Answer:
Attachment is correct graph.
Explanation:
We are given a equation of line y=|x|
It is absolute function which gives always positive value.
It's vertex at (0,0). This function will break at (0,0)
It is linear equality.
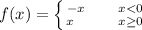
So, function is break at point x=0
Now we make tale of x and y
x y
-3 3
-2 2
-1 1
0 0
1 1
2 2
3 3
Now we plot the point on graph and join the points to get graph.
Please see the attachment for correct graph.