Question

Which coordinate pair identifies the center of the circle represented by 4x2 + 4y2 − 16x − 24y + 36 = 0.

A) (2, 3)
B) (3, 2)
C) (0, 0)
D) (−3, 2)

Answer 1

Option A is correct

Coordinate pair identifies the center of the circle is, (2 , 3)

Explanation:

the general equation of the circle is given by :

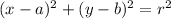`(x-a)^2+(y-b)^2=r^2` ; where (a, b) represents the coordinates of the circle and r is the radius of the circle.

Given :
`4x^2+4y^2-16x-24y+36=0`

`4x^2-16x+4y^2-24y+36=0`

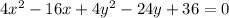
Take common 4 from above equation we have:

`4(x^2-4x+y^2-6y+9=0)`

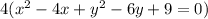
Divide both sides by 4 we get;

`x^2-4x+y^2-6y+9=0`

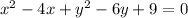
Add and subtract 4 in above equation:

`x^2-4x+y^2-6y+9+4-4=0`

`x^2-4x+4+y^2-6y+5=0`

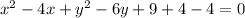
Add and subtract 9 in above equation:

`x^2-4x+4+y^2-6y+5+9-9=0`

`x^2-4x+4+y^2-6y+9-4=0`

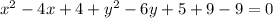
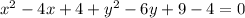
or

`x^2-4x+2^2+y^2-6y+3^2 = 4`

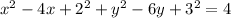
Using identity:
`(a-b)^2 = a^2 - 2ab + b^2`

`(x-2)^2+(y-3)^2 = 2^2`

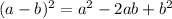
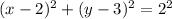
On comparing with the general equation of the circle we have;

a = 2 , b= 3 and r = 2

Therefore, the coordinate pair identifies the center of the circle is, (2 , 3)