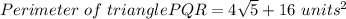Question

Find the perimeter of the following isosceles triangle. show work

Answer 1

Find out the perimeter of the isosceles triangle.

To prove

As shown in the figure.

P(0,4) , Q(-2,0) and R(2,0) are the vertices of the triangle PQR.

Formula

`Distance\ formula = \sqrt{(x_(2) - x_(1))^(2) +(y_(2) -y_(1))^(2)}`

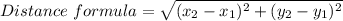
As P(0,4) and Q(-2,0)

`PQ = \sqrt{(-2 - 0)^(2) +(0 - 4)^(2)}`

`PQ = √(4+16)`

`PQ = √(20)\unit`

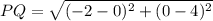
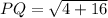
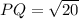
In the isoceles triangle the two sides of the triangles are equal .

Therefore PQ = PR

`PR = √(20)\unit`

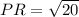
As Q(-2,0) and R(2,0)

`QR = \sqrt{(2- (-2))^(2) +(0 - 0)^(2)}`

`QR = \sqrt{(4)^(2)}`

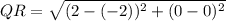
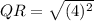
QR = 16 unit

`Perimeter\ of\ triangle PQR = √(20) +√(20) + 16`

`Perimeter\ of\ triangle PQR = 4√(5) + 16\ units^(2)`